Double pendulum model and animation - Is the model correct? - Messages
Hi friends!
Now I am on the forum again!
Anime2.sm (55.59 KiB) downloaded 257 time(s).
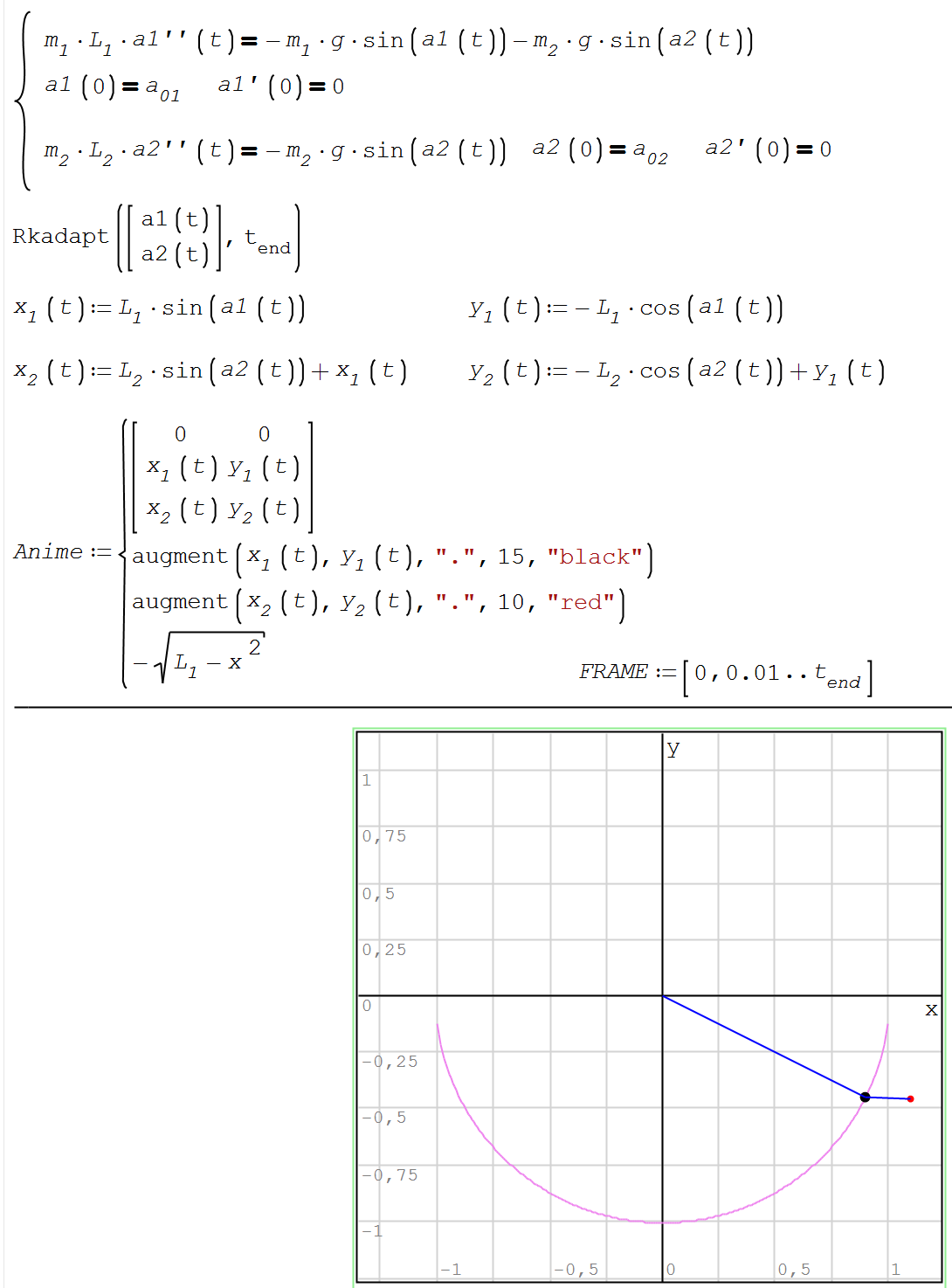
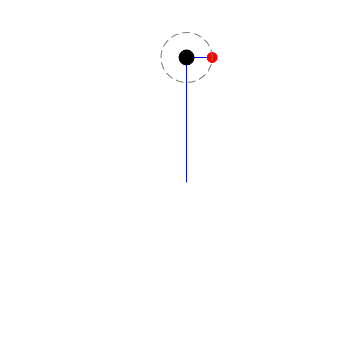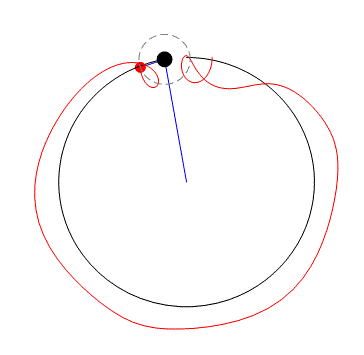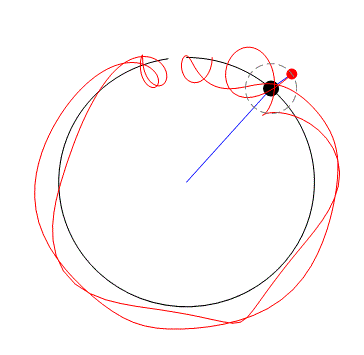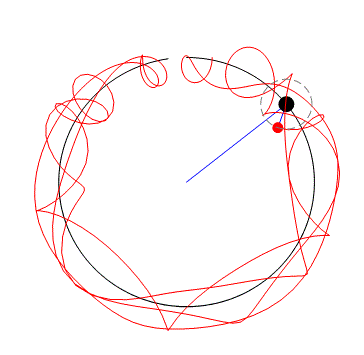
But the model is not correct. See please Alvaro model!
Now I am on the forum again!
Anime2.sm (55.59 KiB) downloaded 257 time(s).

But the model is not correct. See please Alvaro model!
Edited 2025/10/30 19:22:14
Russia ☭ forever, Viacheslav N. Mezentsev
2 users liked this post
Слава, а когда этот новая версия плагина появилась?
Hi. My approach to solving the double pendulum problem.
double_pendulum.sm (75.92 KiB) downloaded 304 time(s).
Best regards.
Alvaro.

double_pendulum.sm (75.92 KiB) downloaded 304 time(s).
Best regards.
Alvaro.
3 users liked this post
Вячеслав Мезенцев 2025/10/30 09:13:40, sergio 2025/10/30 12:18:26, Valery Ochkov 2025/10/30 07:45:32
Triple pendulum - see errors at the second haft of time interval.
Pendulum-3-for-SMath.xmcd (220.62 KiB) downloaded 267 time(s).
Pendulum-3-for-SMath.xmcd (220.62 KiB) downloaded 267 time(s).

Edited 2025/10/30 19:39:16
1 users liked this post
Alvaro 2025/10/31 05:05:16
Hi. Using pure SMath code to deduce the equations of motion from the Lagrangian, with the functions in this post: https://smath.com/en-US/forum/topic/AeeMSM/Using-differentials.

double_pendulum_lagrangian.sm (174.64 KiB) downloaded 245 time(s).
double_pendulum_lagrangian.pdf (503.4 KiB) downloaded 151 time(s).
Best regards.
Alvaro.

double_pendulum_lagrangian.sm (174.64 KiB) downloaded 245 time(s).
double_pendulum_lagrangian.pdf (503.4 KiB) downloaded 151 time(s).
Best regards.
Alvaro.
2 users liked this post
WroteTriple pendulum - see errors at the second haft of time interval.
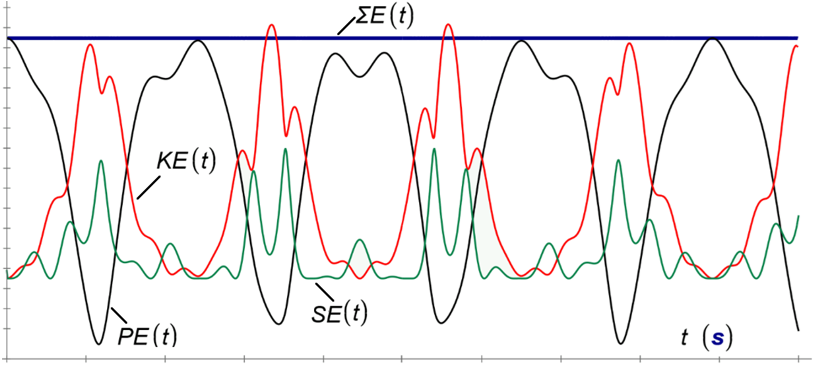
I no longer use Mathcad, except on rare occasions, when I rely on Mathcad version 11, which I consider the last decent version. So I can't see the triple pendulum file. And I suppose this is the situation for many SMath users who no longer have Mathcad readily available. But more than worrying about the conservation of energy, which seems to be a problem with the numerical method used, I'm more surprised to see how the future affects the past, since the animation shouldn't alter the trajectories already described by the particles as time passes.
This is my approach to the triple pendulum.

triple_pendulum_lagrangian.sm (135.01 KiB) downloaded 242 time(s).
triple_pendulum_lagrangian.pdf (248.09 KiB) downloaded 178 time(s).
Best regards.
Alvaro.
Edited 2025/10/31 06:13:23
2 users liked this post
Wrote
I no longer use Mathcad,
See pls pdf
Pendulum-3-for-SMath.pdf (589.25 KiB) downloaded 151 time(s).
Edited 2025/10/31 07:38:52
WroteSee pls pdf
With those values:
triple_pendulum_lagrangian.sm (159.26 KiB) downloaded 249 time(s).
Best regards.
Alvaro.
1 users liked this post
Valery Ochkov 2025/10/31 10:39:04
WroteWrote
I'm more surprised to see how the future affects the past, since the animation shouldn't alter the trajectories already described by the particles as time passes.
Best regards.
Alvaro.
For me too!
Alvaro, hi!
Is it posibble to solve the single pendulun problem with Lagrangian and rkfixed but without the al_nleqsolve function?
Is it posibble to solve the single pendulun problem with Lagrangian and rkfixed but without the al_nleqsolve function?
Edited 2025/11/5 08:29:15
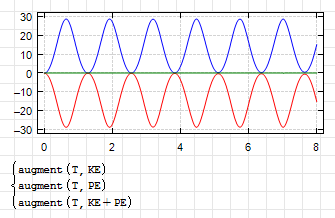
Hi Valery. For the single pendulum you can get the lagrangian from the olf post about differentials ( https://smath.com/en-US/forum/topic/AeeMSM/Using-differentials ) It's very simple and doesn't require much processing to use rkfixed.
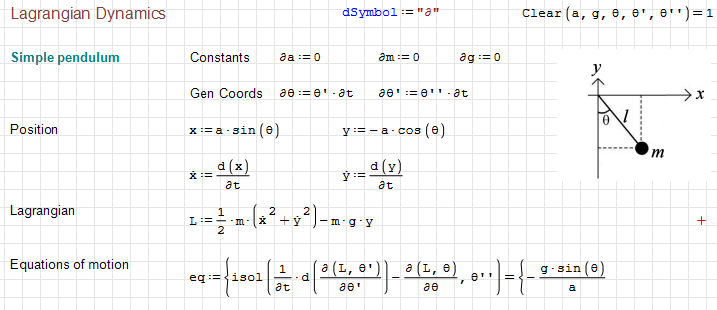
For the double pendulum, you can use Newton-Raphson to solve the system within the function D. Here, a very simple version of the method is used.
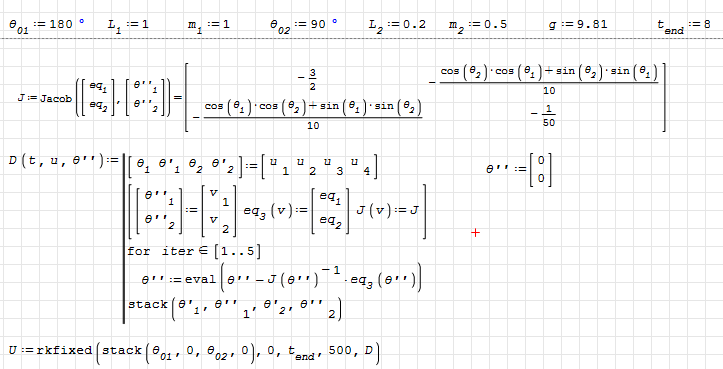
double_pendulum_lagrangian-NR.sm (178.15 KiB) downloaded 229 time(s).
Something similar applies to the pendulum with a spring. Note that the Lagrange equations become somewhat complicated because I use the x,y coordinates to calculate the kinetic energy, and SMath cannot simplify trigonometric functions. However, if you use r, θ' (in green), the equations of motion are greatly simplified. But that breaks the principle that the program should do the calculations, not the user.

Best regards.
Alvaro.
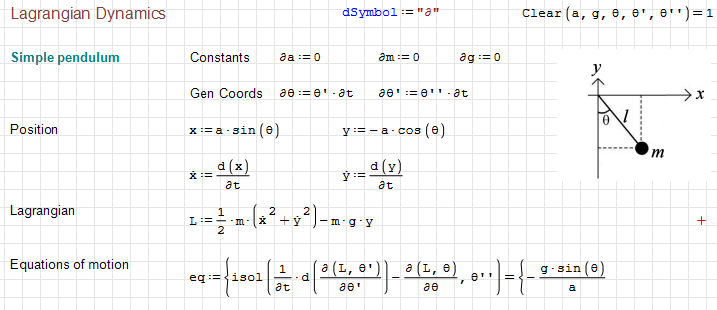
For the double pendulum, you can use Newton-Raphson to solve the system within the function D. Here, a very simple version of the method is used.
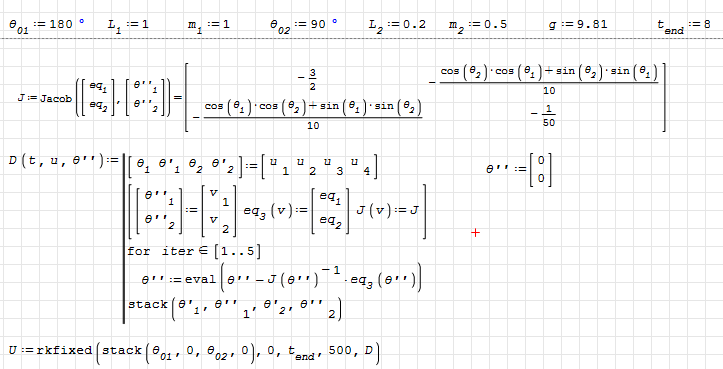
double_pendulum_lagrangian-NR.sm (178.15 KiB) downloaded 229 time(s).
Something similar applies to the pendulum with a spring. Note that the Lagrange equations become somewhat complicated because I use the x,y coordinates to calculate the kinetic energy, and SMath cannot simplify trigonometric functions. However, if you use r, θ' (in green), the equations of motion are greatly simplified. But that breaks the principle that the program should do the calculations, not the user.

Best regards.
Alvaro.
1 users liked this post
Valery Ochkov 2025/11/6 05:16:18
WroteHi Valery. For the single pendulum you can get the lagrangian from the olf post about differentials ( https://smath.com/en-US/forum/topic/AeeMSM/Using-differentials ) It's very simple and doesn't require much processing to use rkfixed.
Alvaro.
Hi Alvaro!
Can you create this simple sm-file with animation? Single pendulum!
Thanks!
- New Posts
- No New Posts