DotNumerics - SMath

#21 Posted: 2018/8/1 12:54:24

1,532 likes in 1,838 posts.

Group: Moderator

Simple test 2.

DotNumerics.ode.test2.sm (21.23 KiB) downloaded 958 time(s).
DotNumerics.ode.test2.pdf (79.99 KiB) downloaded 466 time(s).

Russia ☭ forever, Viacheslav N. Mezentsev

2 users liked this post

sergio 2018/8/1 18:06:00, Radovan Omorjan 2018/8/2 03:05:00

#22 Posted: 2018/8/1 21:57:14

Jean Giraud

983 likes in 6,866 posts.

Group: User

Wrote
Simple test 2.

Works nice conventional/visual [6179].
That document, if it would come from other designer
would pass my QA [Quality Assurance].

Jean

DotNumerics.ode.test2.sm (24.51 KiB) downloaded 1002 time(s).

#23 Posted: 2018/9/9 14:23:36

Martin Kraska

1,308 likes in 2,221 posts.

Group: Moderator

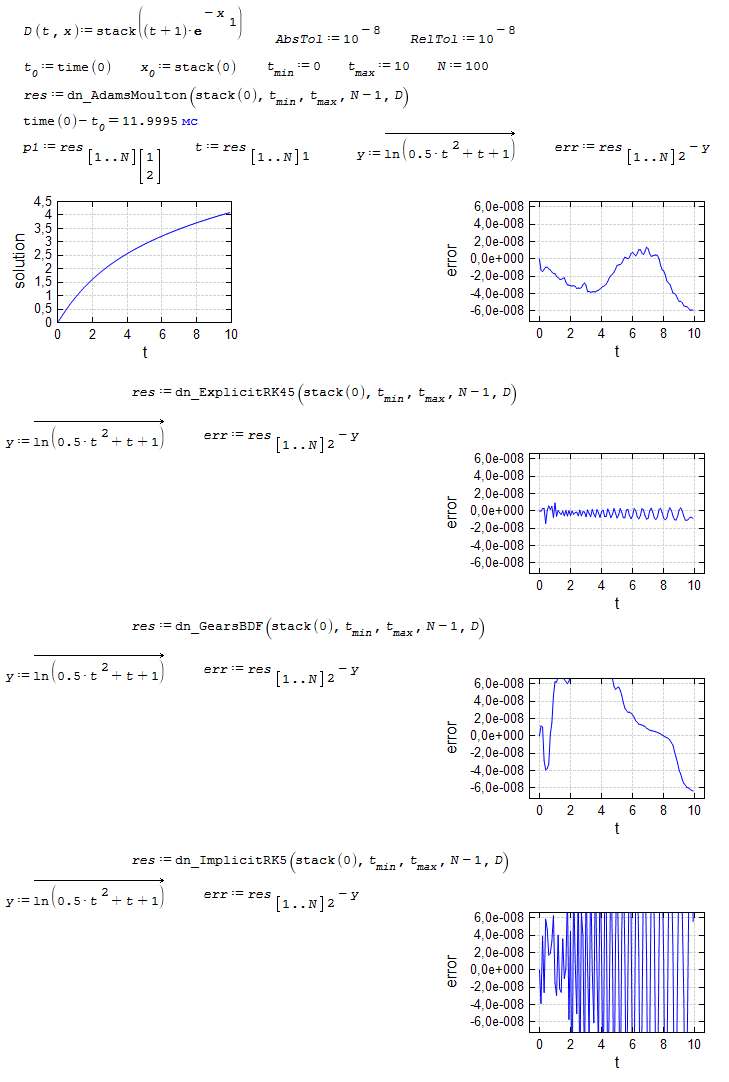
It seems that all the dotnumeric ode solver functions fail to add the last step to the solution. In the given example, the exact solution is (approximately) met if the end value of x is increased by one step (x_end/steps).

The sheet is easily extended to whatever ode solvers by adding their name to the search list. The actually available solvers depend on what plugins are installed.

Section Math ODE precision.sm (23.66 KiB) downloaded 1022 time(s).
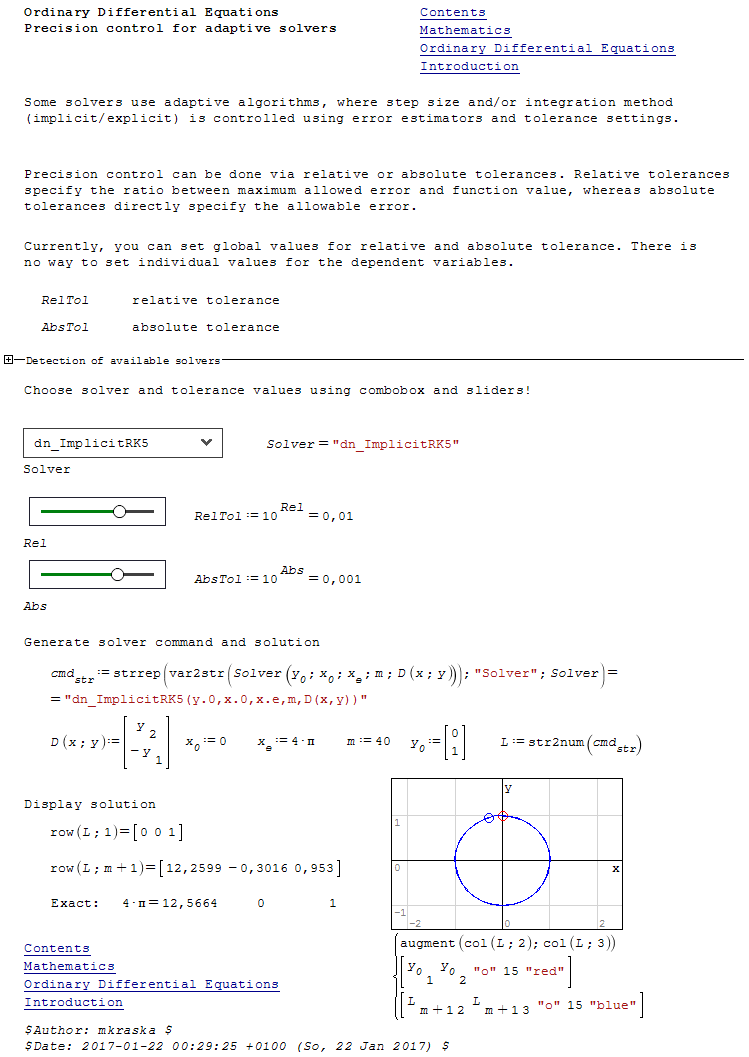
$Section Math ODE precision.png$

Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx

2 users liked this post

frapuano 2018/9/9 17:18:00, Вячеслав Мезенцев 2018/9/10 05:37:00

#24 Posted: 2018/9/10 06:48:25

Вячеслав Мезенцев

1,532 likes in 1,838 posts.

Group: Moderator

Updated for SS 0.99.6824. Intervals issue fixed.

Russia ☭ forever, Viacheslav N. Mezentsev

3 users liked this post

sergio 2018/9/10 07:02:00, frapuano 2018/9/10 09:23:00, NDTM Amarasekera 2018/9/10 09:48:00

#25 Posted: 2018/12/6 14:42:53

Вячеслав Мезенцев

1,532 likes in 1,838 posts.

Group: Moderator

Updated.

Changes:
- zero point issue fixed;
- added support for the simple D(t,x) definition.

Russia ☭ forever, Viacheslav N. Mezentsev

#26 Posted: 2018/12/24 09:13:53

Вячеслав Мезенцев

1,532 likes in 1,838 posts.

Group: Moderator

Updated.

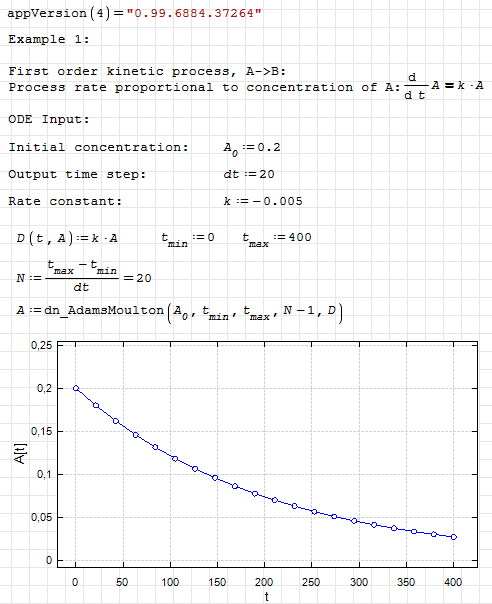
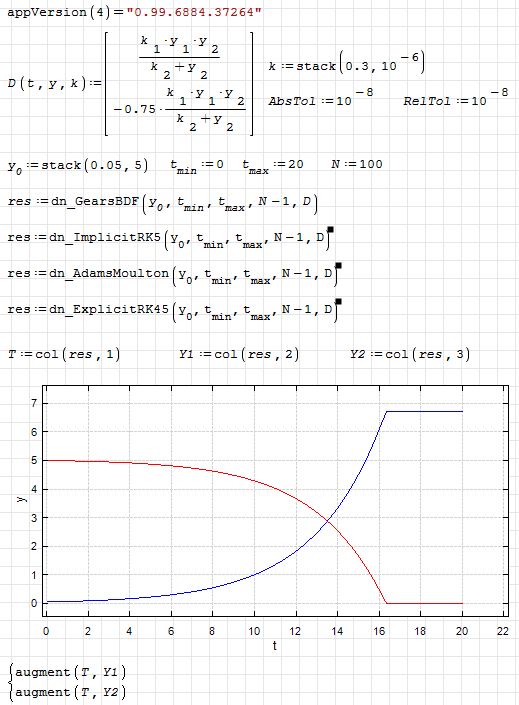
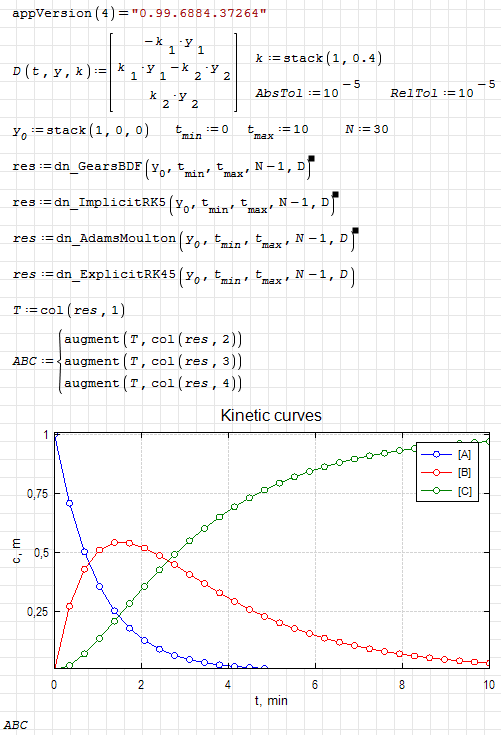
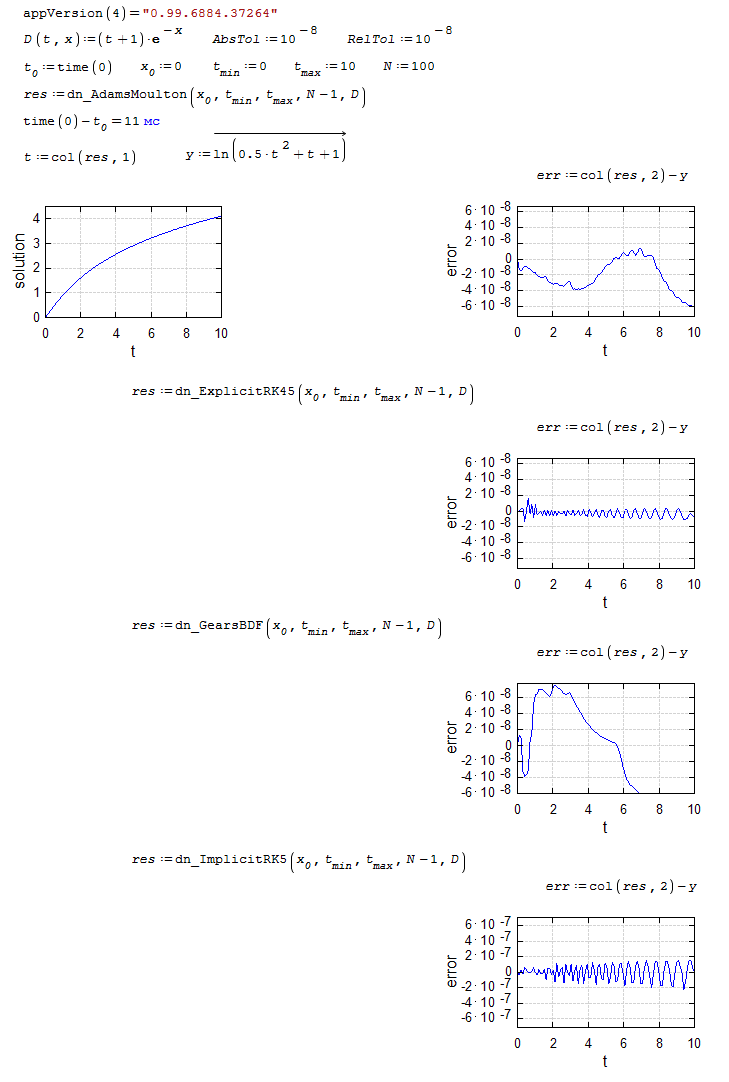
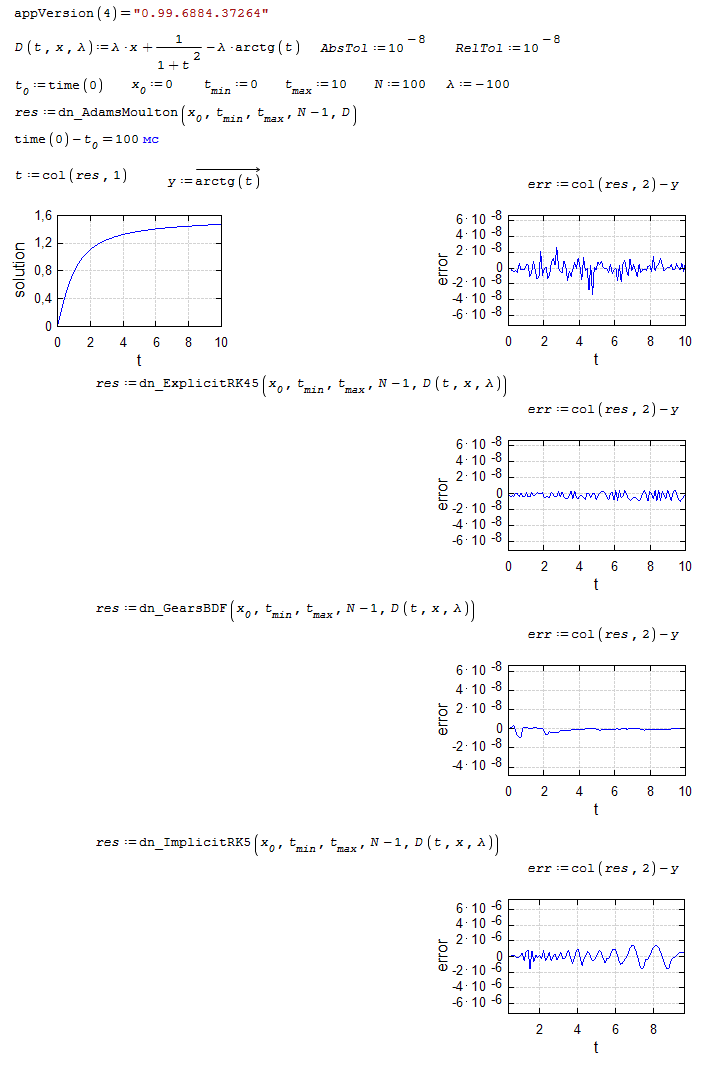
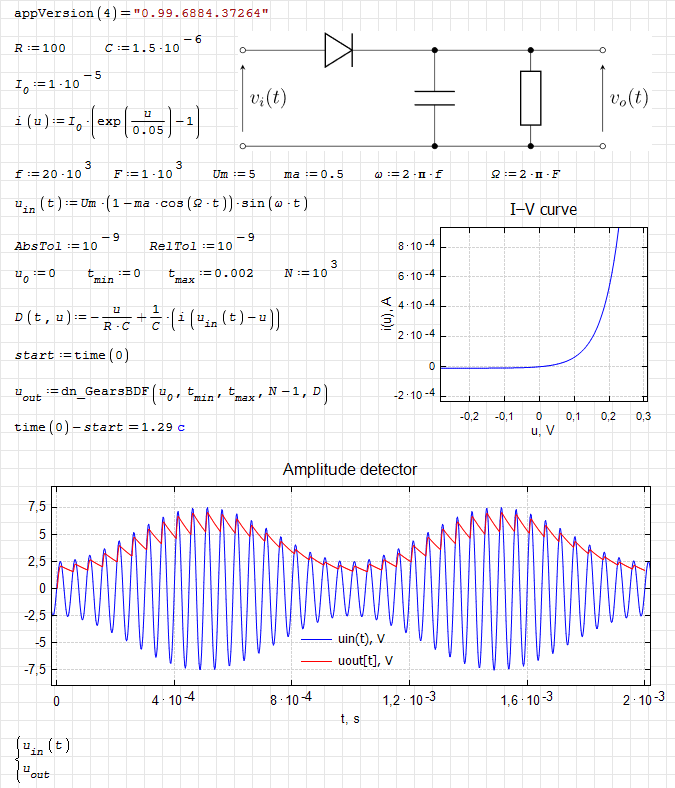
dn.ode.kinetic1.sm (8.26 KiB) downloaded 1103 time(s).
dn.ode.kinetic2.sm (12.59 KiB) downloaded 1047 time(s).
dn.ode.kinetic3.sm (12.28 KiB) downloaded 1043 time(s).
dn.ode.test1.sm (19.58 KiB) downloaded 1051 time(s).
dn.ode.test2.sm (18.88 KiB) downloaded 1064 time(s).
dn.ode.Amplitude detector.sm (20.17 KiB) downloaded 1060 time(s).

dn.ode.kinetic1.pdf (77.42 KiB) downloaded 557 time(s).
dn.ode.kinetic2.pdf (93.05 KiB) downloaded 546 time(s).
dn.ode.kinetic3.pdf (91.31 KiB) downloaded 531 time(s).
dn.ode.test1.pdf (115.72 KiB) downloaded 539 time(s).
dn.ode.test2.pdf (120.44 KiB) downloaded 530 time(s).
dn.ode.Amplitude detector.pdf (148.87 KiB) downloaded 531 time(s).

Russia ☭ forever, Viacheslav N. Mezentsev

4 users liked this post

NDTM Amarasekera 2018/12/24 09:44:00, sergio 2018/12/24 11:04:00, frapuano 2018/12/24 14:23:00, Radovan Omorjan 2018/12/24 14:52:00

#27 Posted: 2018/12/25 14:49:08

Jean Giraud

983 likes in 6,866 posts.

Group: User

Native works as well.
You can try rkfixedSteven.

#28 Posted: 2018/12/25 16:25:11

Jean Giraud

983 likes in 6,866 posts.

Group: User

Read + interesting stuff.

Chemical Kinetics: Introduction with Mathcad/Maple/MCS. Chapter 3

1 users liked this post

frapuano 2018/12/25 19:01:00

#29 Posted: 2021/12/9 09:10:25

Вячеслав Мезенцев

1,532 likes in 1,838 posts.

Group: Moderator

Plugin updated.

Changes:

- added support the mathematical form of the problem for ODE solvers;
- refactored.

Russia ☭ forever, Viacheslav N. Mezentsev

1 users liked this post

sergio 2021/12/9 11:40:00

#30 Posted: 2021/12/20 16:18:13

Вячеслав Мезенцев

1,532 likes in 1,838 posts.

Group: Moderator

Plugin updated.

Changes:

- solution restructured;
- converting the task for the ODE solver to the numerical form is now performed through the Mathcad Toolbox plugin (to avoid code duplication), so it must be installed;
- refactored.

Solvers that support mathematical notation now reuse code from the Mathcad Toolbox plugin. Now there is no need to recompile every such plugin.

Russia ☭ forever, Viacheslav N. Mezentsev

#31 Posted: 2022/8/21 02:43:28

Alvaro

1,078 likes in 1,749 posts.

Group: User

Hi Viacheslav. There are an issue with Implicit and dn_ExplicitRK45, just in the first element. Please see the attached.

dn_ExplicitRK45 issue.sm (8.42 KiB) downloaded 910 time(s).

Best regards.
Alvaro.

1 users liked this post

Вячеслав Мезенцев 2022/8/22 03:11:00

#32 Posted: 2022/8/22 03:12:45

Вячеслав Мезенцев

1,532 likes in 1,838 posts.

Group: Moderator

Plugin updated.

Changes:

- fixed values of initial conditions in the output array for dn_ImplicitRK5() and dn_ExplicitRK45().

Russia ☭ forever, Viacheslav N. Mezentsev

2 users liked this post

sergio 2022/8/22 04:19:00, Alvaro 2022/8/23 20:15:00

SMath Forum

DotNumerics - Initial-value problem for nonstiff and stiff ordinary differential equations ODEs - Messages