1 Pages (4 items)
Matrix Mirror - Matrix Mirror - Messages
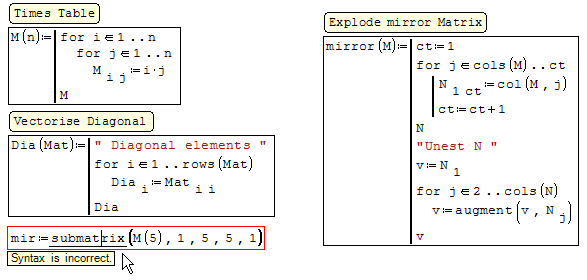
Smath does not support reverse cols order in "submatrix".
Alternately, here is the module. Read more in the attached.
Jean
Utilities Matrix Mirror Exercise.sm (19.08 KiB) downloaded 773 time(s).
Alternately, here is the module. Read more in the attached.
Jean

Utilities Matrix Mirror Exercise.sm (19.08 KiB) downloaded 773 time(s).
I think this is remedied as well with the recent vector indices.
Moreover, I think we can forget about submatrix() function now
http://smath.info/cloud/worksheet/uRMs2euU
Regards,
Radovan
Moreover, I think we can forget about submatrix() function now
http://smath.info/cloud/worksheet/uRMs2euU
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
You even don't have to wait for the vector indices, at least for the mirror.
See here
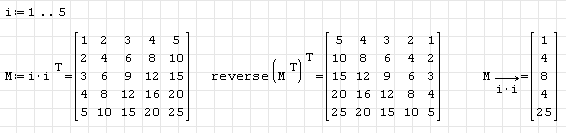
The mirror implementation is straightforward to understand (transpose, reverse, transpose)
The diagonal is a nasty indexing trick, which is that far from paper and pencil notation that it can't be recommended unless you want to obfuscate your algorithm (then best use excel). You just square the row/column index range elements to access the diagonal elements in linear indexing.
This, however, uses the vector index feature.
See here
The mirror implementation is straightforward to understand (transpose, reverse, transpose)
The diagonal is a nasty indexing trick, which is that far from paper and pencil notation that it can't be recommended unless you want to obfuscate your algorithm (then best use excel). You just square the row/column index range elements to access the diagonal elements in linear indexing.
This, however, uses the vector index feature.
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
1 users liked this post
frapuano 2016/9/9 14:23:00
WroteThe diagonal is a nasty indexing trick, which is that far from paper and pencil notation that it can't be recommended unless you want to obfuscate your algorithm (then best use excel). You just square the row/column index range elements to access the diagonal elements in linear indexing.
This, however, uses the vector index feature.
diagonal(M):el(M,(range(0,(rows(M)-1)))*(rows(M)+1)+1)
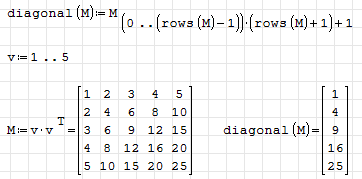
С уважением,
Михаил Каганский
1 users liked this post
NDTM Amarasekera 2016/9/11 15:38:00
1 Pages (4 items)
- New Posts
- No New Posts
