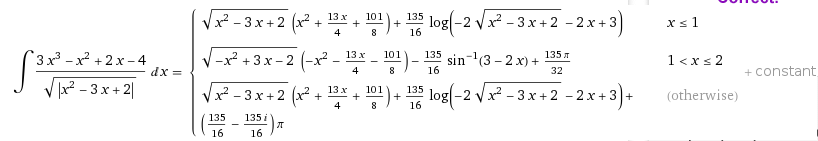1 Pages (11 items)
Definite integral - "x - not defined" ? - Messages
Hello,
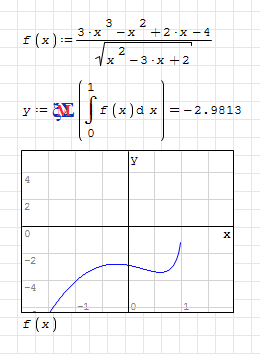
I have the following problem, trying to solve the definite integral int((3*x^3-x^2+2*x-4)/sqrt(x^2-3*x+2),dx,0,1): I get the error "x - not defined" and, of course, no result.
If I change the limits to [0..401], I get a result (!) with no error message, but if I set the upper limit lower than 401, I get the error again...
What is the reason for that?
Thanks in advance for your replies.
Conrad
I have the following problem, trying to solve the definite integral int((3*x^3-x^2+2*x-4)/sqrt(x^2-3*x+2),dx,0,1): I get the error "x - not defined" and, of course, no result.
If I change the limits to [0..401], I get a result (!) with no error message, but if I set the upper limit lower than 401, I get the error again...
What is the reason for that?
Thanks in advance for your replies.
Conrad
WroteThe integrand is undefined @ x = 1
Three verdicts in there:
1. Nothing will integrate that freak above x=1.9999999999999999999999999999
2. Nothing will integrate up to x=0.99999999999999999999999999999999
3. Can only integrate in reasonable range of the integrand.
Interesting Classroom example ... always plot the integrand !!!
IntegrateFreak.sm (7.28 KiB) downloaded 653 time(s).
Hello Conrad,
Often, it is possible to improve the Smath native Simpson integrator.
Romberg is profitable in example 2 which looks easy from plotting
the integrand, but finally is not so.
Jean
Integrate Romberg Technical.sm (51.89 KiB) downloaded 655 time(s).
Often, it is possible to improve the Smath native Simpson integrator.
Romberg is profitable in example 2 which looks easy from plotting
the integrand, but finally is not so.
Jean
Integrate Romberg Technical.sm (51.89 KiB) downloaded 655 time(s).
Hi. I think that here the point is how to handle avoidable discontinuities in SMath. Because integral and other operators or functions not accept the 'if' statement, you can use 'cases' in the definition of f, as this:
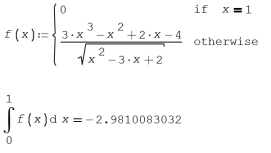
Even this isn't the case, this other is more general for avoiding numerical issues with avoidable discontinuities:
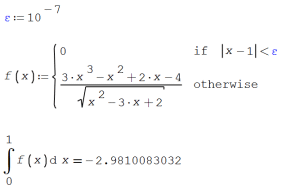
Best regards.
Alvaro.
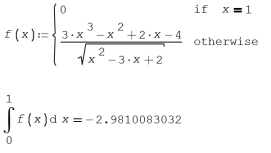
Even this isn't the case, this other is more general for avoiding numerical issues with avoidable discontinuities:
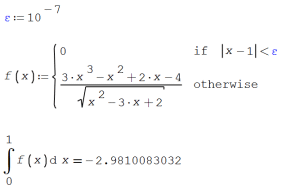
Best regards.
Alvaro.
1 users liked this post
sergio 2019/2/8 08:59:00
About the other discontinuity, at x=2, I guess that you don't want to work with complexes. It's usual take the absolute vale of logs and roots in real analysis calculus. This other isn't avoidable discont, but can be handled in a similar way.
discont_integral.sm (8.65 KiB) downloaded 662 time(s).
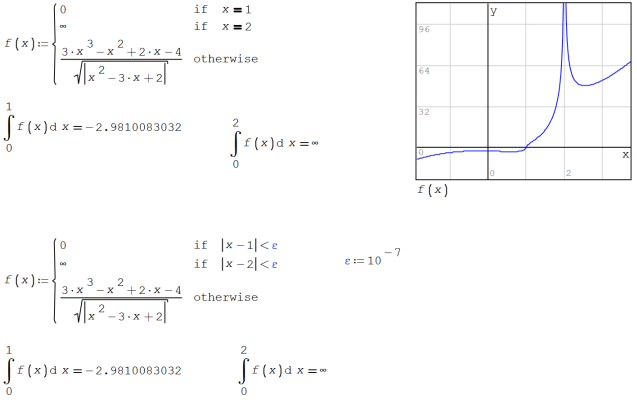
Best regards.
Alvaro.
discont_integral.sm (8.65 KiB) downloaded 662 time(s).
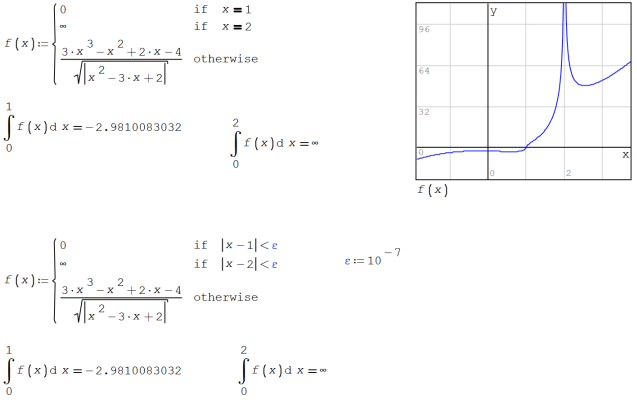
Best regards.
Alvaro.
3 users liked this post
maple() also can do that.
File not found. File not found.
File not found. File not found.
Russia ☭ forever, Viacheslav N. Mezentsev
2 users liked this post
Wrotemaple() also can do that.
maple [0..1] = -2.98126694400594
Mathcad 11 [0..1]= -2.98126694400554
Smath = -2.98126668567898 ... acc 10000
This is a case of singular end point
WroteThat's means that numerical procedure for computing int in SMath needs some improvements.
That's an old long due request.
At least, we have the adaptive from Carlos
Romberg algo style works well, very useful too.
1 Pages (11 items)
- New Posts
- No New Posts