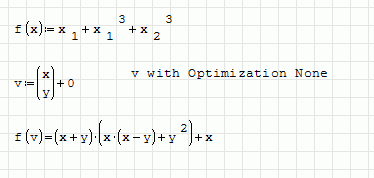1 Pages (9 items)
Hessian - Messages
:d
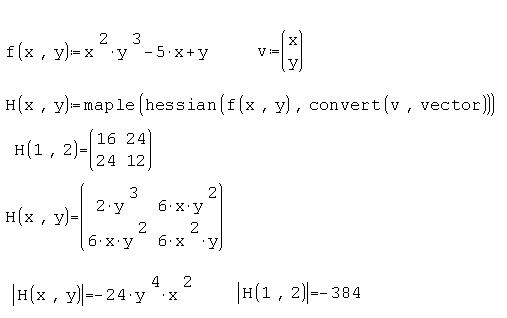
Russia ☭ forever, Viacheslav N. Mezentsev
1 users liked this post
Radovan Omorjan 2012/10/2 03:04:00
I think that this is the better way to work with the Jacobian.
Alvaro.
Jacobian.sm (22.57 KiB) downloaded 943 time(s).
Alvaro.
Jacobian.sm (22.57 KiB) downloaded 943 time(s).
Hello Alvaro,
But what to do if the vector function is defined this way?
[MATH=eng]Φ(X,t):-5*t*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1)^2,2,1)[/MATH]
It will not work until t is a constant (scalar). Take a look at the pictures please.
Regards,
Radovan

But what to do if the vector function is defined this way?
[MATH=eng]Φ(X,t):-5*t*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1)^2,2,1)[/MATH]
It will not work until t is a constant (scalar). Take a look at the pictures please.
Regards,
Radovan

When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
Hello Alvaro,
Actually, that is the point. I think that's the problem of the symbolic engine.
The first one gives the symbolic result
[MATH=eng](-5*t)*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(-5*el(X,1),-5*el(X,2),2,1)*t+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)[/MATH]
and the result is not a vector, therefore length() does not work.
The second one actually give you the vector symbolically
[MATH=eng](-5)*mat(el(X,1)*t,el(X,2)*t,2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(el(X,1)*(-5*t+el(X,2)*el(X,1)),el(X,2)*(-5*t+el(X,2)*el(X,1)),2,1)[/MATH]
Maybe the solution would be to say in advance what the variable t was - either scalar, vector or matrix. Something like "assume". If SMath assumed that t was a scalar, it should behave in accordance to that and give you the second correct result.
Regards,
Radovan
Actually, that is the point. I think that's the problem of the symbolic engine.
The first one gives the symbolic result
[MATH=eng](-5*t)*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(-5*el(X,1),-5*el(X,2),2,1)*t+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)[/MATH]
and the result is not a vector, therefore length() does not work.
The second one actually give you the vector symbolically
[MATH=eng](-5)*mat(el(X,1)*t,el(X,2)*t,2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(el(X,1)*(-5*t+el(X,2)*el(X,1)),el(X,2)*(-5*t+el(X,2)*el(X,1)),2,1)[/MATH]
Maybe the solution would be to say in advance what the variable t was - either scalar, vector or matrix. Something like "assume". If SMath assumed that t was a scalar, it should behave in accordance to that and give you the second correct result.
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
1 Pages (9 items)
- New Posts
- No New Posts