1 Pages (5 items)
Tetrahedron Inertia Tensor - Maxima's use for the subject and a demand for the extension on the general Polyhedral 3D Objects - Messages
#1 Posted: 2/15/2026 12:59:53 PM
Hello Everybody,
I found a very interesting paper about the explicit formulas for the inertia tensor of a tetrahedron, defined with the 3 coordinates of its 4 vertices:
https://thescipub.com/abstract/jmssp.2005.8.11
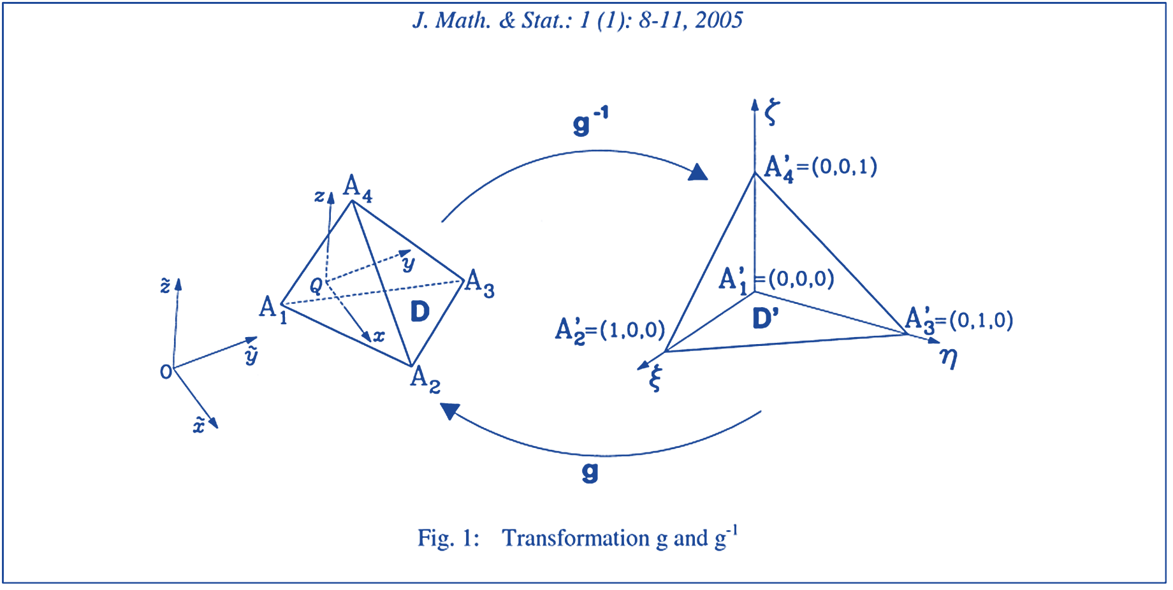
The symbolic integration process for the obtention of the inertia tensor’s terms was conducted in the “F. Tonon’s” paper by using the “Mathematica” program.
I used the “SMath’ Maxima plugin” for the symbolic integrations.
My results gave identical numerical results as that of the “F. Tonon’s” example.
My formulas are available in an appended SMath file:
### Tetrahedron's Inertia Tensor - Ioan 2026.sm (3.04 MiB) downloaded 135 time(s).
I included some additional results obtained by using “Maxima” plugin, for “Eigenvalues and Eigenvectors”. Even if the “Maxima” plugin allows the obtention of symbolic results, the complexity of these formulas lets me prefer the numerical application.
I’m interested in having opinions of those familiar with this category of problems by looking in two directions:
Best Regards,
Ioan
I found a very interesting paper about the explicit formulas for the inertia tensor of a tetrahedron, defined with the 3 coordinates of its 4 vertices:
https://thescipub.com/abstract/jmssp.2005.8.11

The symbolic integration process for the obtention of the inertia tensor’s terms was conducted in the “F. Tonon’s” paper by using the “Mathematica” program.
I used the “SMath’ Maxima plugin” for the symbolic integrations.
My results gave identical numerical results as that of the “F. Tonon’s” example.
My formulas are available in an appended SMath file:
### Tetrahedron's Inertia Tensor - Ioan 2026.sm (3.04 MiB) downloaded 135 time(s).
I included some additional results obtained by using “Maxima” plugin, for “Eigenvalues and Eigenvectors”. Even if the “Maxima” plugin allows the obtention of symbolic results, the complexity of these formulas lets me prefer the numerical application.
I’m interested in having opinions of those familiar with this category of problems by looking in two directions:
a) the connection between the “Eigenvalues and Eigenvectors” results and the rotation classical procedure for the Inertia Moments Tensor.
b) Could it be formulated a procedure to find the Inertia Moments Tensor for the general case of Polyhedral Solid, similar to the classical procedure for 2D polygons, very nicely developed by Davide Carpi in the “Properties of generic Polygons” included in the “SMath Examples”. If the polygon problems are enough available in the literature, I do not know similar procedures for 3D polyhedral objects, defined by their vertex’s coordinates.
b) Could it be formulated a procedure to find the Inertia Moments Tensor for the general case of Polyhedral Solid, similar to the classical procedure for 2D polygons, very nicely developed by Davide Carpi in the “Properties of generic Polygons” included in the “SMath Examples”. If the polygon problems are enough available in the literature, I do not know similar procedures for 3D polyhedral objects, defined by their vertex’s coordinates.
Best Regards,
Ioan
Edited 2/15/2026 1:13:56 PM
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
3 users liked this post
#2 Posted: 2/15/2026 3:26:38 PM
Once you have the inertia tensor of a tetrahedron in arbitrary coordinates, then you can compute the inertia of any body that has a surface triangulation (as available in the STL file format) using tetrahedra generated from a surface triangle and some reference point. The orientation of the triangles matters.
I assume that this approach is used in CAD software to compute the mass properties of 3D bodies.
Here is an example of the 2D procedure from my SMath book: https://smath.com/en-US/cloud/worksheet/LWrsp7uo
I assume that this approach is used in CAD software to compute the mass properties of 3D bodies.
Here is an example of the 2D procedure from my SMath book: https://smath.com/en-US/cloud/worksheet/LWrsp7uo
Edited 2/15/2026 3:46:59 PM
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
2 users liked this post
#3 Posted: 2/15/2026 5:27:56 PM
WroteWroteOnce you have the inertia tensor of a tetrahedron in arbitrary coordinates, then you can compute the inertia of any body that has a surface triangulation (as available in the STL file format) using tetrahedra generated from a surface triangle and some reference point. The orientation of the triangles matters.
I assume that this approach is used in CAD software to compute the mass properties of 3D bodies.
Here is an example of the 2D procedure from my SMath book: https://smath.com/en-US/cloud/worksheet/LWrsp7uo
Thank you for the interestings suggestion.
Of course, a 3D space object can be decomposed by using tetrahedrons.
However, 2D figured do not need imperatively to use triangles for making plan figures.
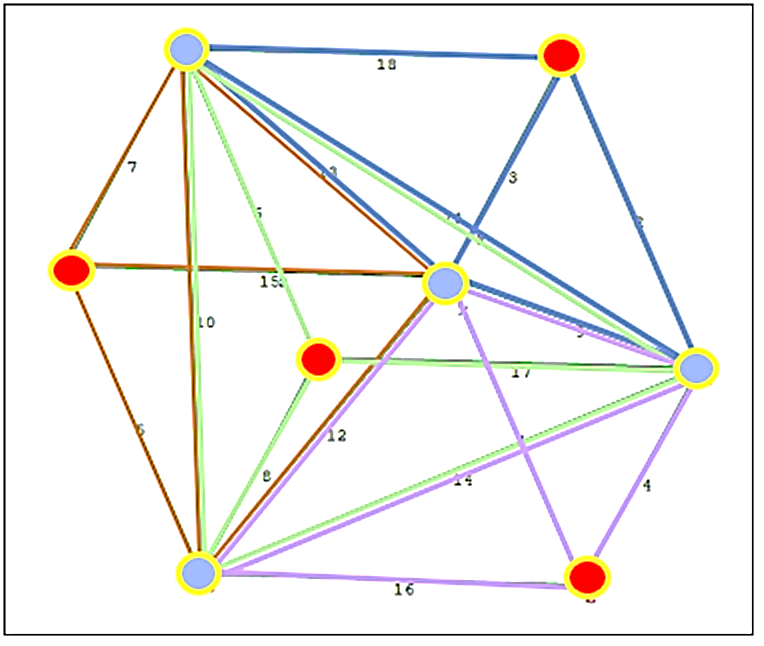
I thought on another nice issues for using tetrahedrons, based on the decomposition of an irregular hexahedron into four linked tetrahedrons as here:
In such way we can create a sort of super element, with an unique output insted of four and also with only 24 input coordinates instead of 6*4*3=72.
The hexahedron finite element is often prefered.
Edited 2/20/2026 2:17:07 PM
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
1 users liked this post
Martin Kraska 2/15/2026 9:21:58 PM
#4 Posted: 2/15/2026 9:21:21 PM
In finite element applications, computing the mass properties (typically represented as mass matrix) is more exciting than just for a rigid body. If you integrate the inertia terms over the volume using the shape functions and gaussian quadrature, you get the consistent mass matrix. Alternatively, you distribute the mass to the nodes and thereby overestimate the rotary intertia of the element.
The tetrahedral decomposition of an arbitrary body with triangular surface tesselation still has the beauty of not needing any internal mesh for computing the mass properties. Just select the reference point (can be outside, can be a surface point) and iterate over the surface triangles.
The tetrahedral decomposition of an arbitrary body with triangular surface tesselation still has the beauty of not needing any internal mesh for computing the mass properties. Just select the reference point (can be outside, can be a surface point) and iterate over the surface triangles.
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
#5 Posted: 2/16/2026 8:51:33 AM
My starting point on this topic was not mainly the Finite Elements, but a problem about the analysis of the "Water ponding on contructions roofs". This problem contains some geometrical nonlinear aspects.
The geometrical properties of 3D objects are widely used also in many other fields ...

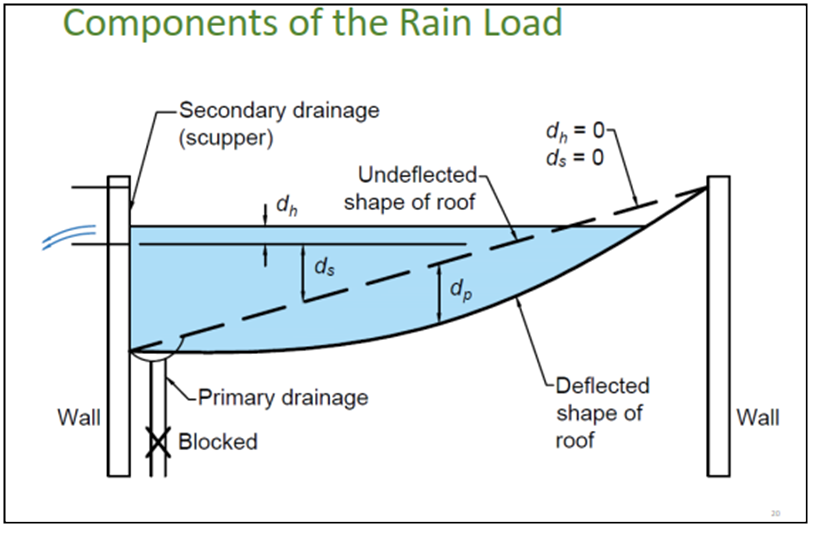

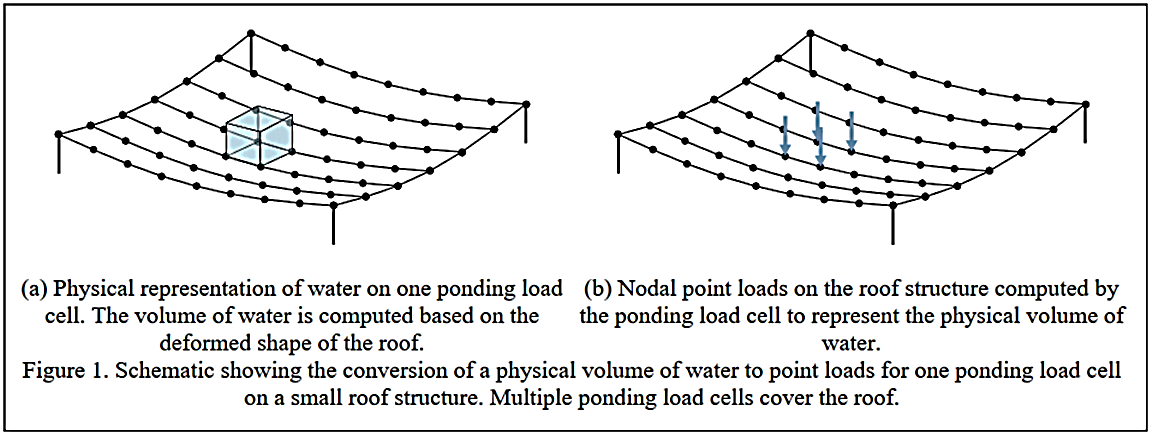
The geometrical properties of 3D objects are widely used also in many other fields ...




Edited 2/16/2026 9:17:59 AM
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
3 users liked this post
1 Pages (5 items)
- New Posts
- No New Posts