Consider the following example. Substitution using at() is applied to a symbolic expression. Once f(t) is not defined, the derivative can't be calculated. It is nice, that t is not just replaced by 0 but the result anyways is not correct. The return value should be the unmodified input expression if evaluation/simplification fails.

You see the problem if you evaluate input and return value for a particular f(x), the results aren't equal.


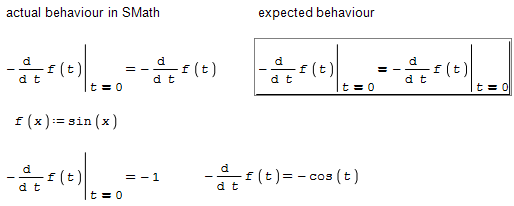
Blatt20.sm (5 КиБ) скачан 70 раз(а).

I don't know what the intention of the author of the at() function is, but what I can observe in other CAS is that there are always something like two versions for the substitution, in which perhaps one maybe returns the expected results.





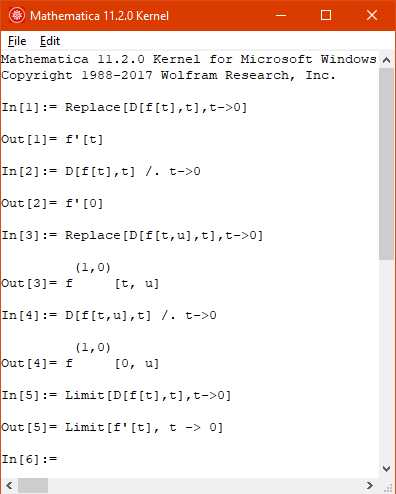
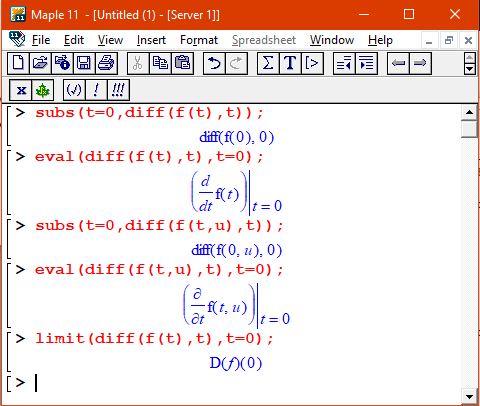
My opinion is that the only procedure about which it can be said that the substitution is correct or not is the limit operation



Maybe Maxima can redefine at() using limits.

Best regards.
Alvaro.

Whatever I do on Maxima side, if the result contains a symbolic non-simplificable substitution (can happen with laplace transforms) then I'd like to display that using the at() function with it's nice operator form to display the result. Yet, as of now, the function isn't robust enough for this.

In the example below you see that the return value from Maxima contains an expression with at(), which is removed on SMath postprocessing side even if optimization=none.
It is part of the test suite for Maxima in the interactive handbook or on github.



The limit function, by the way is another construction site. Currently, it is not possible to use the single-sided limits. We have that on our todo list.

Hi Martin,

I think I can handle it plugin-side, I'll look into it ASAP.

Wrote

You see the problem if you evaluate input and return value for a particular f(x), the results aren't equal.

Pretty obvious that f(x):= sin(0.5*x)
evaluation t=0 will not be same.
Vectorize over t[0,0.125..pi]

By same token of diff at(2)
1. 1rst derivative of erf(x) is the integrand.
that you derive D(n,x) at will, range/vectorize.
2. Derivative of Gamma(x) from infinitesimal analysis.