Thank you very much!

Just for information:
1) Since SMath Studio 0.85 release there is not required to define Vector/Matrix dimensions before elements definitions;
2) eval(..) function can speed up this calculations (on my PC: from 3.3 sec to 0.57 sec).

For more information please, take a look to the screenshot:


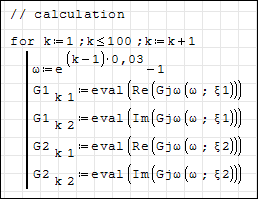
Thanks again. Best regards, Andrey Ivashov.

Hallo Andrey,
thanks for tip with function "eval". After using "eval" function calculation took five time quickly. But I don't understand when shall I use "eval" functin. And what do you mean "define Vector/Matrix dimensions before elements definitions"?

You are welcome.

Wrote

But I don't understand when shall I use "eval" functin

Here is description about eval(..) function from Insert Function Dialog: "Converts analytic expression to the numeric notation."
For example, please, try to define such variable:
[MATH]A←mat(sqrt(3);sin(8);ln(5);e;2;2)^{-1}[/MATH]
If you will check then the numeric result, you'll see this:
[MATH]A=mat(0,8724;-0,3175;-0,5165;0,5559;2;2)[/MATH]
But you should remember, that SMath Studio stores all intermediate calculations in symbols. To see it, just try to get symbolic result (or just hover the A definition by the mouse):
[MATH]A—mat(e/{e*sqrt(3)-ln(5)*sin(8)};-sin(8)/{e*sqrt(3)-ln(5)*sin(8)};-ln(5)/{e*sqrt(3)-ln(5)*sin(8)};sqrt(3)/{e*sqrt(3)-ln(5)*sin(8)};2;2)[/MATH]

So, if you'll try now to calculate, f.e.:
[MATH]B←A^3[/MATH] (Fig. 1)
And to check symbolic result, you'll see this one:
[MATH]B—mat({e*(e^2+sin(8)*ln(5))+(e+sqrt(3))*sin(8)*ln(5)}/{(e*sqrt(3)-ln(5)*sin(8))^3};-{(e^2+sin(8)*ln(5)+(e+sqrt(3))*sqrt(3))*sin(8)}/{(e*sqrt(3)-ln(5)*sin(8))^3};-{(3+ln(5)*sin(8)+e*(e+sqrt(3)))*ln(5)}/{(e*sqrt(3)-ln(5)*sin(8))^3};{(e+sqrt(3))*ln(5)*sin(8)+(3+ln(5)*sin(8))*sqrt(3)}/{(e*sqrt(3)-ln(5)*sin(8))^3};2;2)[/MATH] (Fig. 2)
Numerically it is:
[MATH]B=mat(1,0413;-0,5458;-0,8879;0,4972;2;2)[/MATH] (Fig. 3)

As you can note, all next calculations are become more complex. Of course, to evaluate such big expressions SMath Studio needs a time. But you can ask the program for numerical simplification of the examples. Let's try:
[MATH]B←eval(A^3)[/MATH] (Fig. 1*)
[MATH]B—mat(52063850537761/50000000000000;-545822825158897/1000000000000000;-110989617673979/125000000000000;62147432086303/125000000000000;2;2)[/MATH] (Fig. 2*)
Or numerically:
[MATH]B=mat(1,0413;-0,5458;-0,8879;0,4972;2;2)[/MATH] (Fig. 3*)

Now program don't need to work with log, sin, sqrt and constants - all these represented as numbers. That's how you can save CPU time! But you don't need to use eval(..) everywhere It is useful only when symbolic results are really big!
One more thing about eval - when you converts analytically given expression to numbers, you round it to 15 decimal places, so, in some cases you can get calculations errors. When you use symbols you just cannot get the error in calculations, but it takes more time.

If you still have questions about this, please, ask.

Wrote

And what do you mean "define Vector/Matrix dimensions before elements definitions"?

You don't need to do these:
[MATH]C←matrix(2;3)[/MATH]
[MATH]el(C;2;3)←5[/MATH]
[MATH]C=mat(0;0;0;0;0;5;2;3)[/MATH]
Just:
[MATH]el(C;2;3)←5[/MATH]
[MATH]C=mat(0;0;0;0;0;5;2;3)[/MATH]

This means, that Vectors and Matrices now works like dynamic arrays.

Best regards, Andrey Ivashov.

Thanks for explanation, using of "eval" is clear. Dynamic building of arrays is very interesting, but in my opinion is matrix definition in this case more transparent.
Best Regardes
Standa

Hello Standa,

Wrote

Dynamic building of arrays is very interesting, but in my opinion is matrix definition in this case more transparent.

Could you be more specific, please. I do not understand your point.

Regards,
Radovan

Wrote

Hello Standa,

Wrote

Dynamic building of arrays is very interesting, but in my opinion is matrix definition in this case more transparent.

Could you be more specific, please. I do not understand your point.

Regards,
Radovan

Sorry,
I answered on wrong topic, my answer on this place is nonsense. I thought about Nyquist plot (first and second topic). For understanding there is better first define matrix. Of coarse is posible use dynamic array, as showed Andrey is 2nd topic.

No problem

You can use it in the way you find it more convenient.

Regards,
Radovan