1 Pages (9 items)
Integrating Shear Along the Length of a Beam - Messages
#1 Posted: 10/4/2024 3:46:56 AM
Hello. I'm a long time lurker on this forum, but this is my first post. I'm trying to solve for shear, moment, and deflection along a beam via direct integration and superposition.
The piecewise equation for shear is pretty simple and I am able to plot V(x). But I am running into trouble integrating it to get M(x). I know that the built-in integration tool sometimes has trouble with units, maybe that's the error that I'm running into? I appreciate any help!
For reference, this is what I'm trying to do:
V(x) from beam equations -> M(x) = ∫ V(x) dx -> θ(x) = 1/EI ∫ M(x) dx -> Δ = ∫ θ(x) dx
I am using mkraska's unoffical portable distribution with Maxima (v99.7579), if that matters.
Updated Simple Span Beam Calculator.sm (130 KiB) downloaded 53 time(s).
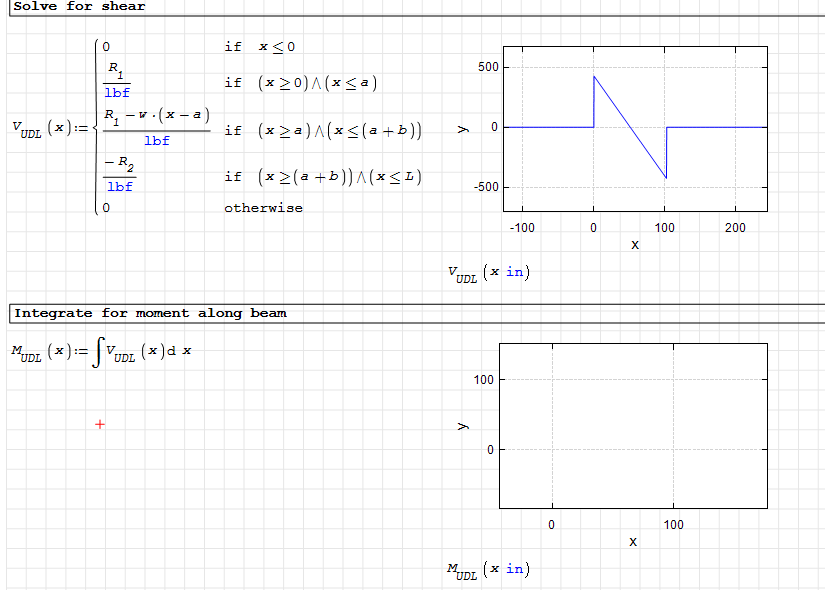
The piecewise equation for shear is pretty simple and I am able to plot V(x). But I am running into trouble integrating it to get M(x). I know that the built-in integration tool sometimes has trouble with units, maybe that's the error that I'm running into? I appreciate any help!
For reference, this is what I'm trying to do:
V(x) from beam equations -> M(x) = ∫ V(x) dx -> θ(x) = 1/EI ∫ M(x) dx -> Δ = ∫ θ(x) dx
I am using mkraska's unoffical portable distribution with Maxima (v99.7579), if that matters.
Updated Simple Span Beam Calculator.sm (130 KiB) downloaded 53 time(s).
#2 Posted: 10/4/2024 5:17:16 PM
The Maxima plugin can't translate boolean expressions and the cases() function.
Therefore, piecewise continuous functions need to be defined using the sign() function, as demonstrated in the attached document (showing shear and bending moment for piecewise continuous distributed load).
You can, however, use the native numeric integrator, yet cascading it is not recommended due to performance reasons.
The noise at the right is a sampling artifact due to the standard 100 integration intervals. Increase the value under Tools> Options to reduce the noise and increase computation time.
Updated Simple Span Beam Calculator (1).sm (133 KiB) downloaded 55 time(s).
![2024-10-04 12_12_04-SMath Solver - [Updated Simple Span Beam Calculator (1).sm_].png](/en-US/file/3H72Kq/2024-10-04-12_12_04-SMath-Solver---_Updated-Simple-Span-Beam-Calculator-_1__sm___png)
Piecewise.pdf (358 KiB) downloaded 56 time(s).
Therefore, piecewise continuous functions need to be defined using the sign() function, as demonstrated in the attached document (showing shear and bending moment for piecewise continuous distributed load).
You can, however, use the native numeric integrator, yet cascading it is not recommended due to performance reasons.
The noise at the right is a sampling artifact due to the standard 100 integration intervals. Increase the value under Tools> Options to reduce the noise and increase computation time.
Updated Simple Span Beam Calculator (1).sm (133 KiB) downloaded 55 time(s).
Piecewise.pdf (358 KiB) downloaded 56 time(s).
Martin Kraska
Pre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#3 Posted: 10/4/2024 9:04:29 PM
SMath doesn't seem to like doing more than one integration here! However, it's easy to do a simple numerical quadrature for theta and delta:
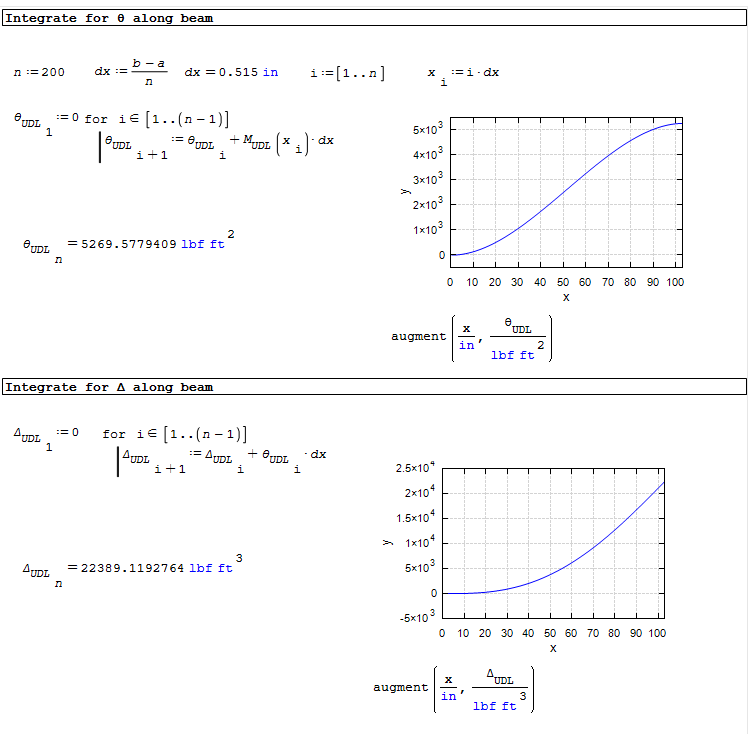
Updated Simple Span Beam Calculator_2.sm (137 KiB) downloaded 55 time(s).
Updated Simple Span Beam Calculator_2.sm (137 KiB) downloaded 55 time(s).
#4 Posted: 10/4/2024 11:07:36 PM
mkraska, when I open your file MUDL doesn't plot and it gives an error: "x' is undefined". All the plugins are enabled and dependencies resolved, but there must be a back compatibility issue with opening your file in an older version. : (
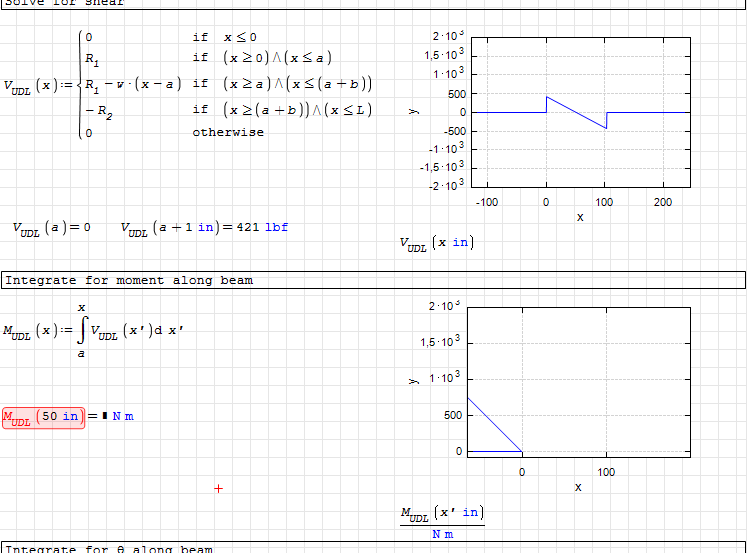
StvMath, I get a similar error with your file: "X is undefined". Also your plots for theta and delta don't match up with what you would expect. For the uniformly distributed load entered at the top of the spreadsheet, delta should be roughly parabolic. Numerical integration gives the values for total area under the curve along the beam, which isn't a helpful value for this use case.
I guess this example gets at my frustration with SMath (at least in an a structural engineering application). I see "what you see is what you get" as being incredibly value for performing "hand calcs" and showing your work, but when something as straightforward as double/triple integration requires setting up loops and/or other non-trivial functions, "what you see" gets obscured from "what you get" and you end up with something like Excel spreadsheets which are intuitive to the person that made them, but impossible to understand for anyone else.
StvMath, I get a similar error with your file: "X is undefined". Also your plots for theta and delta don't match up with what you would expect. For the uniformly distributed load entered at the top of the spreadsheet, delta should be roughly parabolic. Numerical integration gives the values for total area under the curve along the beam, which isn't a helpful value for this use case.
I guess this example gets at my frustration with SMath (at least in an a structural engineering application). I see "what you see is what you get" as being incredibly value for performing "hand calcs" and showing your work, but when something as straightforward as double/triple integration requires setting up loops and/or other non-trivial functions, "what you see" gets obscured from "what you get" and you end up with something like Excel spreadsheets which are intuitive to the person that made them, but impossible to understand for anyone else.
#5 Posted: 10/4/2024 11:30:20 PM
Hi. There are some long discussions here about issues handling piecewise functions for beam calculations. BTW, this could be a way to solve the problem:
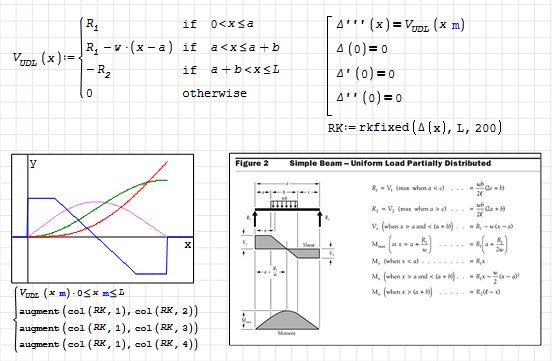
Simple Span Beam Calculator.sm (124 KiB) downloaded 52 time(s).
Further, you can use interpolation for define functions for M, θ and Δ.
Best regards.
Alvaro.
Simple Span Beam Calculator.sm (124 KiB) downloaded 52 time(s).
Further, you can use interpolation for define functions for M, θ and Δ.
Best regards.
Alvaro.
1 users liked this post
sergio 10/5/2024 1:14:00 AM
#6 Posted: 10/5/2024 1:08:40 AM
Razonar, what is that one sided bracket with the initial delta values in it? I am working with an older version of Smath (and older ODE plugin) that doesn't support that element. Trying to find out if there is a way around the unsupported element.
#7 Posted: 10/5/2024 1:37:31 AM
That's a Mathcad block from Viacheslav's Mathcad plugin. This is how to solve with the classical ODE engine
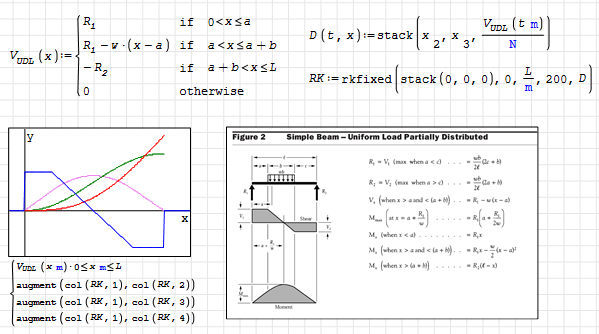
Simple Span Beam Calculator - old version.sm (124 KiB) downloaded 55 time(s).
Best regards.
Alvaro.
Simple Span Beam Calculator - old version.sm (124 KiB) downloaded 55 time(s).
Best regards.
Alvaro.
1 users liked this post
ioan92 10/5/2024 2:51:00 AM
#8 Posted: 10/5/2024 4:35:10 AM
Greetings,
I just wanted to note: Constants matter.
When you integrate for Slope of Deflection and Deflection, you cannot ignore the constants that get generated (e.g. http://www.engineeringcorecourses.com/solidmechanics1/C9-deflection-of-beams-and-shafts/C9.1-integration-method/theory/).
May this be of Good Help;
⚜ Kenny Lemens, P.E. ᵂᴵ
I just wanted to note: Constants matter.
When you integrate for Slope of Deflection and Deflection, you cannot ignore the constants that get generated (e.g. http://www.engineeringcorecourses.com/solidmechanics1/C9-deflection-of-beams-and-shafts/C9.1-integration-method/theory/).
May this be of Good Help;
⚜ Kenny Lemens, P.E. ᵂᴵ
"No matter where you go, there you are." -Buckaroo BanzaiHotkeys: https://en.smath.com/forum/resource.ashx?a=45771&b=2
#9 Posted: 10/5/2024 2:45:20 PM
@willmccartney
StvMath, I get a similar error with your file: "X is undefined". Also your plots for theta and delta don't match up with what you would expect. For the uniformly distributed load entered at the top of the spreadsheet, delta should be roughly parabolic.
"X is undefined" Can't explain this! It works for me. An SMath idiosyncrasy?
Plot for delta. Perhaps we're looking at different curves, as it looks pretty parabolic to me!
StvMath, I get a similar error with your file: "X is undefined". Also your plots for theta and delta don't match up with what you would expect. For the uniformly distributed load entered at the top of the spreadsheet, delta should be roughly parabolic.
"X is undefined" Can't explain this! It works for me. An SMath idiosyncrasy?
Plot for delta. Perhaps we're looking at different curves, as it looks pretty parabolic to me!
1 Pages (9 items)
-
 New Posts
New Posts
-
 No New Posts
No New Posts
